Conteúdos
- Introdução
- Pré-requisitos
- Porquê os algoritmos k-means e DBSCAN?
- O que é agrupamento (clustering)?
- Como funciona o k-Means?
- Quantos agrupamentos devo escolher?
- Como é que o DBSCAN funciona?
- Primeiro caso de estudo: Aplicar k-means ao conjunto de dados de autores da antiguidade do Brill’s New Pauly
- Segundo caso de estudo: agrupamento de dados textuais
- Sumário
- Bibliografia
- Notas de rodapé
Introdução
Este tutorial demonstra como implementar e aplicar o algoritmo k-means e DBSCAN em Python. Os algoritmos k-means e DBSCAN são dois populares métodos de agrupamento de dados que, em combinação com outros, podem ser utilizados durante a fase de análise exploratória dos dados para descobrir estruturas escondidas através da identificação de grupos que partilham atributos similares (ver Patel 2019). Iremos implementar estes algoritmos utilizando scikit-learn. O scikit-learn é uma biblioteca de Python que apresenta boa documentação, sendo utilizada numa grande diversidade de tarefas relacionadas com aprendizagem automática. Assim que a compreensão da implementação dos algoritmos k-means e DBSCAN em scikit-learn for atingida, este conhecimento pode ser facilmente utilizado para implementar outros algoritmos de aprendizagem automática em scikit-learn.
Este tutorial é composto por dois casos de estudo. O primeiro aplica algoritmos de agrupamento ao conjunto de dados de autores da antiguidade retirado da enciclopédia Brill’s New Pauly. O segundo caso de estudo foca-se em aplicar a tarefa de agrupamento a dados textuais, especificamente sobre os abstracts de todos os artigos da publicação científica Religion (Taylor & Francis). Estes dois conjuntos de dados foram selecionados de modo a ilustrar como os algoritmos de agrupamento conseguem trabalhar sobre diferentes tipos de dados (incluindo, por exemplo, variáveis numéricas e textuais), assim como as suas possíveis aplicações a uma diversidade de tópicos de pesquisa.
A próxima secção introduzirá os dois conjuntos de dados.
Primeiro caso de estudo: autores da antiguidade no Brill’s New Pauly
Neste exemplo, vamos utilizar k-means para analisar o conjunto de dados que contém registos sobre 238 autores da antiguidade Greco-romana. Os dados foram retirados do website oficial da Brill’s New Pauly e provêm do Supplement I Volume 2: Dictionary of Greek and Latin Authors and Texts. Der Neue Pauly: Realenzyklopädie der Antike (em Ingês Brill’s New Pauly) (1996–2002) é uma enciclopédia dedicada à antiguidade com contribuições de pesquisadores estabelecidos no panorama internacional. É de notar que o acesso aos textos (e por isso aos dados) contidos no New Pauly não é livre. Utilizei as credenciais de acesso da universidade para obter os dados relativos aos autores. Nas análises subsequentes nenhum dos textos do New Pauly foram copiados para o conjunto de dados. No entanto, os dados numéricos do conjunto de dados foram extraídos e parcialmente acumulados dos registos dos autores no New Pauly. A versão original em alemão foi traduzida para inglês em 2002. Daqui em diante referências ao texto serão feitas através da abreviação DNP.
Este tutorial demonstra como o k-means pode ajudar a agrupar os autores da antiguidade em conjuntos distintos. A ideia geral é que os algoritmos de agrupamento ou nos disponibilizam novas descobertas sobre a estrutura dos nossos dados, ou provam/negam hipóteses existentes. Por exemplo, pode existir um grupo de autores discutidos detalhadamente, mas com poucos manuscritos atríbuídos a eles. Enquanto, outro grupo pode conter autores, com muitos manuscritos conhecidos, mas com poucas entradas no DNP. Outro potencial cenário seria encontrar um grupo de autores associado com muitas edições iniciais, mas apenas algumas modernas. Isto iria, por exemplo, suportar a hipótese que os pesquisadores modernos continuam a utilizar edições antigas quando leem estes autores. No contexto deste tutorial, deixaremos os algoritmos determinar agrupamentos promissores.
Os dados sobre os autores foram recolhidos do website oficial utilizando módulos e bibliotecas de Python, destacando, por exemplo: requests, BeautifulSoup e pandas.1 Os dados foram guardados num ficheiro CSV chamado DNP_ancient_authors.csv (ver o respositório no GitHub).
Um único registo (linha) no ficheiro DNP_ancient_authors.csv contém o nome do autor, como chave, contendo também as seguintes variáveis:
- O número de palavras da entrada no DNP, utilizado como uma medida da importância do autor (
word_count) - Número de traduções modernas (
modern_translations) - Número de trabalhos conhecidos (
known_works) - Número de manuscritos existentes (
manuscripts) - Número de primeiras edições (
early_editions) - Número de primeiras traduções (
early_translations) - Número de edições modernas (
modern_editions) - Número de comentários (
commentaries)
Portanto, um registo do conjunto de dados deve ter este aspeto:
| authors | word_count | modern_translations | known_works | manuscripts | early_editions | early_translations | modern_editions | commentaries |
|---|---|---|---|---|---|---|---|---|
| Aelianus Tacticus | 350 | 1 | 1 | 0 | 3 | 6 | 1 | 0 |
Segundo caso de estudo: abstracts de artigos na publicação Religion
O segundo conjunto de dados contém os abstracts de todos os artigos da publicação Religion (Taylor & Francis). Os abstracts foram recolhidos do website oficial utilizado módulos e bibliotecas de Python tais como requests, BeautifulSoup, pandas. Os dados foram guardados num ficheiro CSV chamado ReligionAbstracts.csv (ver o repositório do GitHub). O conjunto de dados contém os abstracts de 701 artigos publicados em 51 volumes entre 1971 e 2021. No entanto, alguns artigos, particularmente os dos volumes mais antigos, não continham os abstracts num formato que fosse extraível e foram, por isso, deixados de fora. Outros tipos de contribuições como revisões de literatura e outra miscelânea também foram excluídos deste conjunto de dados.
Um único registo (linha) no ficheiro RELIGION_abstracts.csv contém uma chave numérica e as seguintes variáveis:
- O título do artigo (
title) - O abstrato completo (
abstract) - Uma hiperligação para o artigo (
link) - Uma hiperligação para o volume no qual o artigo (abstract) foi publicado (
volume)
Portanto, um registo do conjunto de dados deve ter este aspeto:
| title | abstract | link | volume |
|---|---|---|---|
| Norwegian Muslims denouncing terrorism: beyond ‘moderate’ versus ‘radical’? | In contemporary (…) | https://www.tandfonline.com/doi/full/10.1080/0048721X.2021.1865600 | https://www.tandfonline.com/loi/rrel20?treeId=vrrel20-51 |
A análise neste tutorial foca-se no agrupamento de dados em formato textual guardados na coluna do abstract. Vamos aplicar o algoritmo k-means e DBSCAN para encontrar agrupamentos temáticos incluídos na diversidade de tópicos discutidos na publicação Religion. Para conseguirmos isto, primeiro criaremos uma representação vetorial do documento para cada abstract (através da estatística numérica TF-IDF, Term Frequency - Inverse Document Frequency. Em português: frequência do termo - inverso da frequência nos documentos) para reduzir a dimensionalidade do conjunto de dados, da representação inicial que corresponde à totalidade do vocabulário dos abstratos, para depois procurar agrupamentos temáticos.
Pode descarregar os dois conjuntos de dados, assim como um Jupyter Notebook contento o código que será escrito no decurso deste tutorial, no repositório do GitHub. Esta lição irá funcionar independentemente de sistema operativo, caso siga estas instruções para configurar o ambiente de desenvolvimento com Anaconda ou Google Colab, que permite correr o Jupyter Notebook quer localmente, quer na Cloud.
Pré-requisitos
Para seguir este tutorial deve ter conhecimentos básicos de programação (de preferência Python) e estar familiarizado com as principais bibliotecas de Python, tais como pandas e matplotlib (ou os seus equivalentes em outras linguagens de programação). É preciso também um conhecimento básico de estatísticas descritiva. Por exemplo, deve-se saber o que é a média, o desvio padrão e a diferença entre variáveis categóricas e contínuas.
Porquê os algoritmos k-means e DBSCAN?
Geralmente, pode escolher entre vários algoritmos de agrupamento para analisar os dados, tais como k-means, agrupamento hierárquico, e DBSCAN. Neste tutorial, vamos focar no k-means uma vez que é relativamente fácil de entender, com um tempo de execução rápido e que mesmo assim oferece resultados decentes,2 o que faz com que seja uma excelente modelo inicial. O segundo algoritmo selecionado foi o DBSCAN, uma vez que serve como um excelente acréscimo ao conhecimento do k-means. Além de outras características, o DBSCAN permite focar em agrupamentos densos e não lineares presentes no conjunto de dados, enquanto mantém pontos de dados correspondentes a ruído ou outliers (em português, valores atípicos) fora dos agrupamentos determinados, que é algo que o k-means não é capaz de fazer por si (o k-means mantém os outliers nos k agrupamentos determinados).
No entanto, outros algoritmos de agrupamento podem ser implementados facilmente com o scikit-learn depois de uma familiarização inicial com este fluxo de trabalho. Portanto, se decidir analisar os dados com algoritmos de agrupamento adicionais (tais como agrupamento hierárquico) o mesmo será fácil de realizar após terminar este tutorial. É normalmente aconselhável aplicar mais que um algoritmo de agrupamento para ter diferentes perspetivas do conjunto de dados e para melhor avaliar o resultado do modelo.
O que é agrupamento (clustering)?
O Agrupamento (em inglês, clustering) é uma parte do grande campo que é a aprendizagem automática. Aprendizagem automática é um processo associado ao campo da inteligência artificial através do qual os computadores conseguem aprender os dados sem serem explicitamente programados (ver Géron, 2019). Isto significa que um processo de aprendizagem automática, após ser invocado, consegue descobrir de forma independente estruturas nos dados ou mesmo gerar previsões com base em novos (desconhecidos) dados. O campo da aprendizagem automática pode ser separado em aprendizagem supervisionada, não supervisionada e por reforço (ver Géron 2019).
Aprendizagem supervisionada usa dados rotulados para treinar os algoritmos de aprendizagem automática e realizar previsões fiáveis sobre dados novos. Um bom exemplo é um filtro de spam (com os dados rotulados como ‘spam’ e ‘não spam’). Uma das formas de avaliar a precisão de um modelo supervisionado é testando o mesmo num conjunto de dados que foi pré-rotulado, comparando as previsões do modelo e dos rótulos originais. Entre outras coisas, a precisão de um modelo depende da quantidade e qualidade dos dados rotulados sobre os quais foi treinado, assim como o valor definido para os parâmetros da técnica de modelação (ajuste dos hiperparâmetros). Para construir um modelo supervisionado decente é necessário um ciclo contínuo de treino, teste, e afinar os hiperparâmetros do modelo. Alguns exemplos de classificadores supervisionados incluem k-vizinhos mais próximos (‘k-nearest neighbors’, (KNN)) e regressão logística.
Apredizagem não supervisionada usa dados não rotulados. Entre outras coisas, é utilizada para detetar anomalias, redução de dimensionalidade, e agrupamento. Quando utilizamos algoritmos de aprendizagem não supervisionada não alimentamos o nosso modelo com dados pré-rotulados para fazer previsões. Queremos antes que o modelo detete potenciais estruturas nos nossos dados. Os conjuntos de dados deste tutorial são um bom exemplo disto: treinamos o nosso modelo ou sobre o autor, ou sobre o abstract, e esperamos que o modelo indique onde (potenciais) agrupamentos existem, (por exemplo, os artigos na publicação Religion com tópicos similares). O ajuste dos hiperparâmetros também é parte integrante de aprendizagem não supervisionada; no entanto, nestes casos, os resultados da tarefa de agrupamento não podem ser comparados com nenhuns dados previamente rotulados. No entanto, existem algumas medidas aplicáveis, tais como o método do cotovelo (‘elbow’) ou o coeficiente de silhueta para avaliar o resultado de variar os diferentes parâmetros (tal como o número de agrupamentos no k-means).
Aprendizagem por reforço é um tipo de aprendizagem que é menos relevante para pesquisadores na área de humanidades. Aprendizagem por reforço consiste em criar um agente (por exemplo, um robô) que pode realizar um conjunto de ações, sendo que pode ser recompensado ou punido pela sua execução. O agente aprende então a reagir ao seu ambiente de acordo com o resultado das suas ações anteriores.
Como funciona o k-Means?
Em seguida apresentamos uma visão geral do funcionamento do algoritmo k-means, focando no naïve k-means, no qual os centros dos agrupamentos (centroides) são inicializados de forma aleatória. No entanto, a implementação do k-means no scikit-learn utilizada neste tutorial integra muitas melhorias ao algoritmo original. Por exemplo, ao invés de distribuir de forma aleatória os centros dos agrupamentos (centroides) o modelo utiliza uma estratégia diferente chamada k-means++, que é uma forma mais inteligente de distribuir os centroides iniciais. No entanto, o funcionamento do k-means++ está fora do âmbito deste tutorial, recomendando a leitura deste artigo pelo David Arthur e Sergei Vassilvitskii para saber mais.
O algoritmo k-means
Para explicar como o k-means funciona comecemos com apenas uma parte do nosso conjunto de dados DNP_ancient_authors.csv. Posteriormente, incluiremos mais variáveis, mas é útil focarmos em algumas variáveis-chave nesta secção introdutória para explicar como esta técnica de agrupamento funciona.
| authors | word_count | known_works |
|---|---|---|
| Aelianus Tacticus | 350 | 1 |
| Ambrosius | 1221 | 14 |
| Anacreontea | 544 | 1 |
| Aristophanes | 1108 | 11 |
Para começar com o agrupamento k-means é preciso primeiro definir o número de agrupamentos que queremos encontrar nos nossos dados. Na maioria das situações não é possível saber à partida quantos agrupamentos existem, por isso a questão de escolher um número inicial apropriado para os agrupamentos é complicada. Iremos posteriormente debruçar-nos sobre este problema, mas comecemos por rever o funcionamento geral do k-means.
O algoritmo consiste em dois passos. O primeiro é medir a distância entre cada ponto no conjunto de dados e o centro atual dos agrupamentos (no nosso caso, através da distância euclidiana \(\sqrt[]{(x_1-x_2)^{2}+(y_1-y_2)^{2}} \), onde ( (x_1,y_1) ) e ( (x_2,y_2) ) são dois pontos no nosso espaço bidimensional). Depois, cada ponto de dados é atribuído ao agrupamento do centroide que menos dista.
O segundo passo consiste em criar novos centroides calculado a média de todos os pontos de dados atribuídos a cada centroide.
Após criar os novos centroides, o algoritmo recomeça o processo de associar cada ponto de dados ao centroide mais próximo. O algoritmo pára quando os centroides estão mais ou menos estáveis. A visualização da página da wikipedia para o algoritmo *k-means* é útil para compreender este processo de dois passos.
O gráfico com os resultados do agrupamento sobre a parte do conjunto de dados DNP_ancient_authors é o seguinte, incluindo a posição final dos centroides:
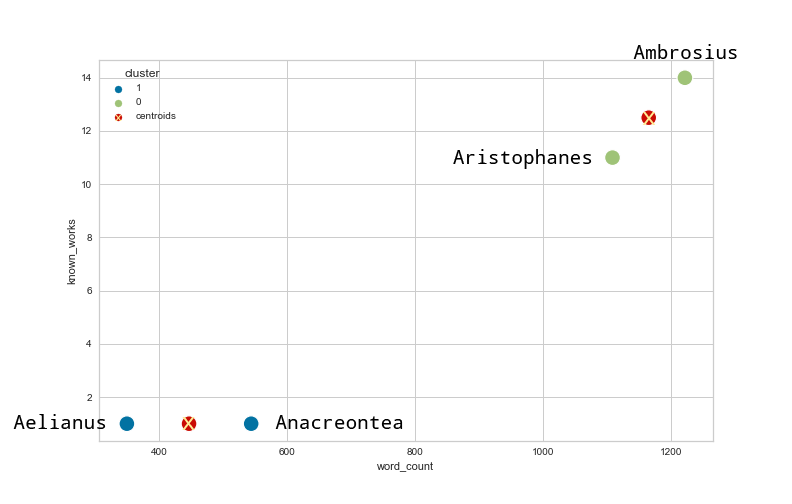
Figura 1: Os dados dos autores da antiguidade agrupados e os centroides obtidos pelo algoritmo k-means representados num espaço bidimensional.
Este resultado parece ser satisfatório. Podemos rapidamente ver que os centroides estão posicionados entre os pontos de dados que assumimos intuitivamente representar um só agrupamento. No entanto, podemos notar que as escalas nos eixos diferem significativamente. No eixo dos y valores variam entre 1 e 15, enquanto no eixo dos x a escala representa valores entre 300 e 1300. Por isso, uma mudança no eixo dos x provavelmente influencia mais a distância entre os pontos de dados que uma mudança no eixo dos y. Isto tem impacto na determinação dos centroides e por isso no processo de construir os agrupamentos. Para mostrar este problema mudemos então o número de palavras associados a Aristophanes de 1108 para 700.
| authors | word_count | known_works |
|---|---|---|
| Aelianus Tacticus | 350 | 1 |
| Ambrosius | 1221 | 14 |
| Anacreontea | 544 | 1 |
| Aristophanes | 700 | 11 |
Se aplicarmos o algoritmo k-means no conjunto de dados mudado, obtemos o seguinte resultado?
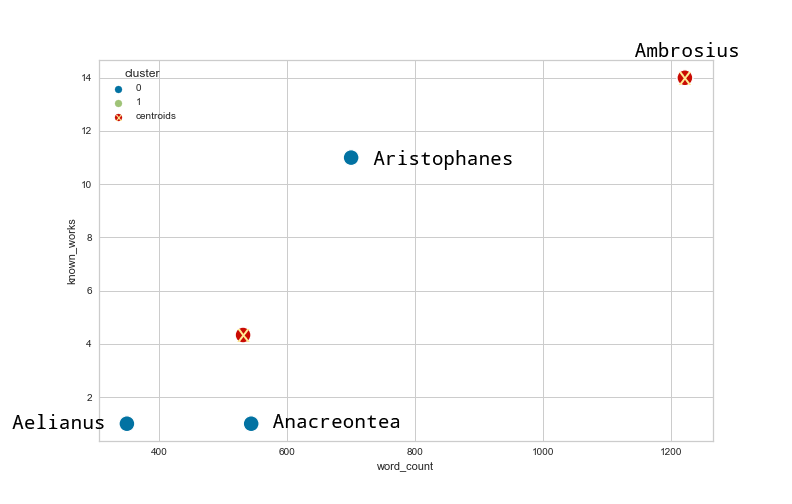
Figura 2: A nova versão dos dados agrupados e dos respetivos centroides utilizando o algoritmo k-means sobre os dados mudados dos autores da antiguidade.
Como podem ver a mudança na contagem de palavras resultou num novo agrupamento com três autores que têm aproximadamente o mesmo número de palavras associado no DNP, mas que têm números muito diferentes de trabalhos publicados. Será que isto faz sentido? Não seria mais razoável deixar Ambrosius e Aristophanes no mesmo agrupamento uma vez que eles têm aproximadamente o mesmo número de trabalhos documentados? De modo a ter em conta estes problemas das diferentes escalas é recomendável normalizar os dados antes de realizar o agrupamento. Existem diferentes formas de fazer isto, entre elas a normalização min-max ou a normalização z-score, que também pode ser designada de padronização. Neste tutorial vamos focar-nos na última. Isto significa, que em cada registo do conjunto de dados, o valor de cada variável tem de ser subtraido pela média dos valores para essa variável e dividido pelo desvio padrão das mesmas. Felizmente, o skikit-learn já nos fornece uma implementação destas técnicas de normalização, removendo a necessidade para o seu cálculo manual.
O conjunto de dados dos autores da antiguidade normalizado (z-score) tem este aspeto:
| authors | word_count | known_works |
|---|---|---|
| Aelianus Tacticus | -1.094016 | -0.983409 |
| Ambrosius | 1.599660 | 1.239950 |
| Anacreontea | -0.494047 | -0.983409 |
| Aristophanes | -0.011597 | 0.726868 |
Agora se aplicarmos k-means ao conjunto de dados normalizado, o resultado que obtemos é o seguinte:
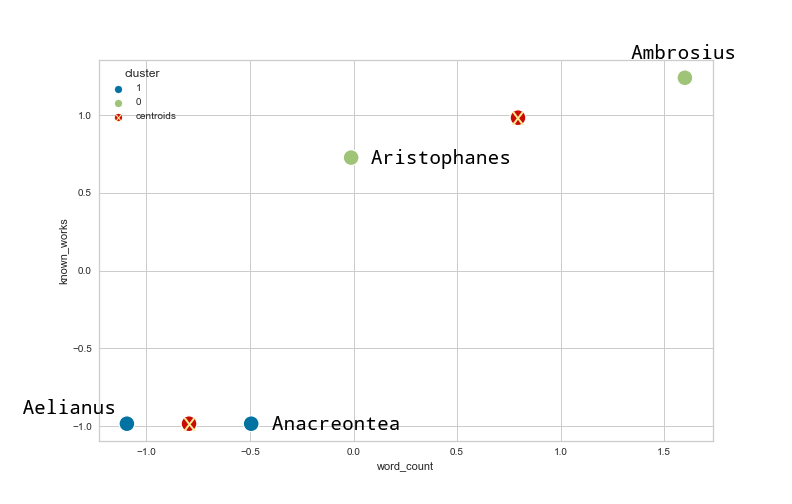
Figure 3: O resultado do agrupamento utilizando o k-means no conjunto de dados normalizado.
Como é possível verificar, mudar o número de palavras tem agora menos influência no resultado do agrupamento. No nosso exemplo, trabalhar com conjuntos de dados normalizados é a forma mais apropriada de agrupar os dados, caso contrário a variável known_works iria perder muito do seu valor na análise realizada.
Quantos agrupamentos devo escolher?
Método do cotovelo (‘elbow’)
A questão de quantos centroides escolher é difícil. Não existe nenhuma solução padrão para este problema. No entanto, algumas medidas de desempenho podem dar uma ajuda para escolher o número de agrupamentos adequado aos dados. Um exemplo útil é o método do cotovelo, que será aquele que utilizaremos neste tutorial. O método do cotovelo tem como base a medição da inércia dos agrupamentos para números de agrupamentos variáveis. Neste contexto, a inércia é definida como:
A soma do quadrado das distâncias dos pontos de dados ao seu centroide mais próximo.3
A inércia diminui com o aumento do número de agrupamentos. Num extremo a inércia será zero, isto acontece quando o número de agrupamentos iguala o número de pontos de dados no conjunto. Mas como é que esta informação pode ajudar a encontrar o número adequado de agrupamentos? Idealmente, existe uma expectativa que a inércia diminua de forma menos acelerada a partir de um determinado número de agrupamentos (n) para a frente, de modo que um gráfico (fictício) da relação entre a inércia e o número de agrupamentos (‘clusters’) teria o seguinte aspeto?
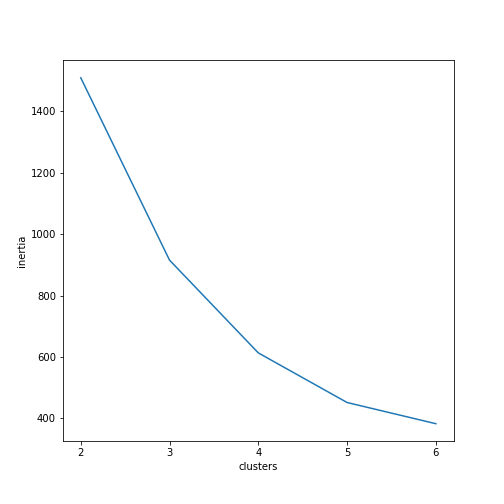
Figura 4: Exemplo fictício do gráfico da inércia pelo número de agrupamentos
Neste gráfico o ‘cotovelo’ é encontrado para quatro agrupamentos. Isto indica que quatro agrupamentos podem ser considerados com um balanço razoável entre relativa baixa inércia (os pontos designados a cada um dos agrupamentos não estão muito longe do centroide) e um baixo número de agrupamentos. Novamente, este método apenas fornece uma ideia de um ponto inicial para a investigação. A decisão final depende de cada um e é altamente influenciada pelos dados em questão e a questão de pesquisa. Descobrir o número adequado de agrupamentos deve ser acompanhado por outros passos, tais como representar graficamente os dados e avaliar outras estatísticas. Na aplicação prática de k-means iremos ver como utilizar a inércia para descobrir o número adequado de cluster para o nosso conjunto de dados DNP_anciente_authors.csv.
Coeficiente de silhueta
Outra forma de avaliar o agrupamento dos dados é utilizando o índice de silhueta, um método que permite avaliar o grau de qualidade de associação de cada ponto de dados com o seu agrupamento atual. Uma forma de perceber o funcionamento do índice de silhueta é lendo o artigo da Wikipedia relativo ao mesmo Silhouette (clustering):
O valor de silhueta é uma medida que avalia quão similar é um objeto em relação ao seu agrupamento (coesão) quando comparado com outros agrupamentos (separação). Os valores assumidos pelo índice de silhueta variam entre -1 e 1, onde um valor alto indica que o objeto é similar a outros do seu agrupamento e dissimilar relativamente aos agrupamentos vizinhos. Se a maioria dos objetos tiver um valor elevado, então a configuração dos agrupamentos é apropriada. Quanto mais pontos tiverem um valor baixo ou negativo, mais provável é que a configuração ou poucos ou demasiados agrupamentos.
Neste tutorial, utilizaremos o coeficiente de silhueta com a biblioteca Python de visualização de aprendizagem automática yellowbrick. Representar a média do valor de silhueta para todos os agrupamentos relativamente a cada um do valor de silhueta médio de cada um dos agrupamentos pode ajudar a avaliar a qualidade do modelo e a adequação da escolha atual de valores para os parâmetros.
Para ilustrar como um gráfico de silhueta pode ajudar a encontrar o número correto de agrupamentos nos dados, podemos realizar uma demonstração baseada no nosso conjunto de dados de autores da antiguidade. Os dados são baseados numa amostra fictícia do número de autores e obras conhecidas de um conjunto de autores. Os dados já foram normalizados utilizando o z-score.
| authors | known_works | word_count |
|---|---|---|
| Author A | 0.24893051 | 0.83656758 |
| Author B | 0.38169345 | 0.04955707 |
| Author C | 0.11616757 | 0.34468601 |
| Author D | -0.01659537 | 0.14793338 |
| Author E | -1.21146183 | -1.18014685 |
| Author F | -1.07869889 | -1.27852317 |
| Author G | -0.94593595 | -1.22933501 |
| Author H | -1.07869889 | -1.1309587 |
| Author I | -0.68041007 | -0.34394819 |
| Author J | -0.81317301 | -0.83582976 |
| Author K | -0.41488419 | -0.54070081 |
| Author L | -0.54764713 | -0.43838945 |
| Author M | 1.1782711 | 1.62357809 |
| Author N | 1.31103404 | 1.52520177 |
| Author O | 1.57655992 | 1.41698783 |
| Author P | 1.97484874 | 1.03332021 |
Podemos agora representar graficamente o coeficiente de silhueta para números variáveis de agrupamentos, n. Neste exemplo, representemos o coeficiente de silhueta para dois, três e quatro agrupamentos utilizando o k-means?
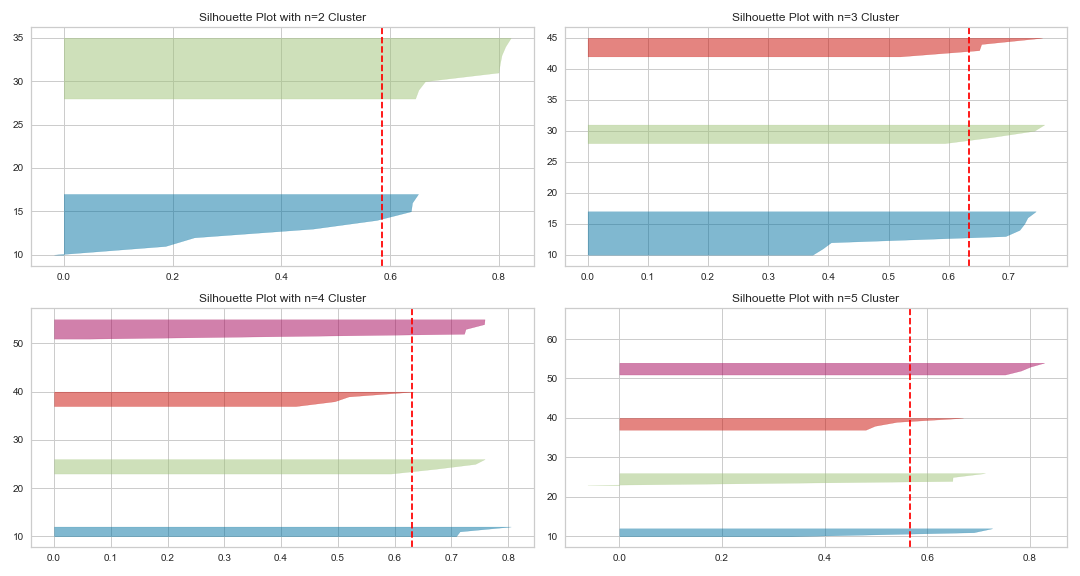
Figura 5: Os gráficos de silhueta utilizando k-means para n agrupamentos entre dois e cinco.
A linha tracejada vertical indica o valor da silhueta médio de todos os pontos de dados. As ‘facas’ horizontais representam a distribuição dos valores de silhueta para todos os pontos num agrupamento em ordem descendente. Os gráficos mostram-nos que um número de agrupamentos entre quatro e cinco parece ser o mais apropriado para o nosso conjunto de dados. Particularmente os pontos para quatro agrupamentos aparentam ter um relativamente elevado coeficiente de silhueta médio (maior que 0.6) e as ‘facas’ aparentam ter aproximadamente o mesmo tamanho e não são demasiado afiadas, o que indica que a coesão intra-agrupamento não é má. De facto, se representarmos os nossos dados utilizando o k-means para n=4 agrupamentos, podemos verificar que esta escolha é razoável oferecendo uma boa ideia sobre a distribuição dos pontos de dados.
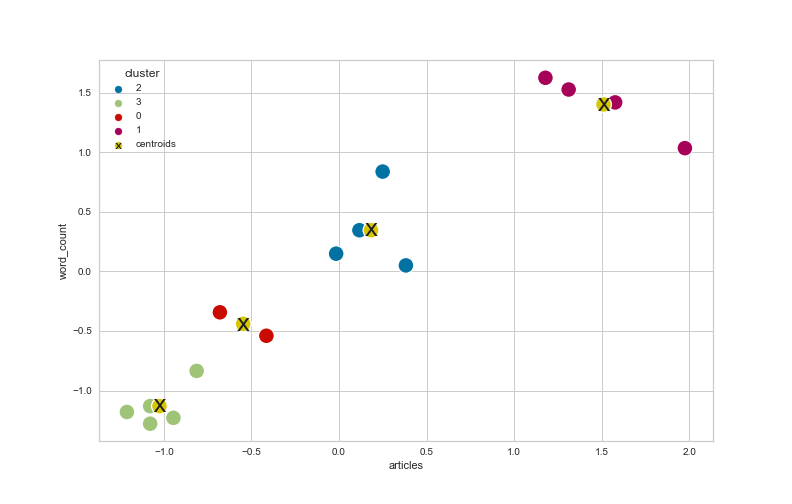
Figura 6: O gráfico de dispersão do conjunto de dados utilizando o k-means para n=4 agrupamentos.
Como é que o DBSCAN funciona?
DBSCAN significa ‘Density-based Spatial Clustering of Applications with Noise’ (agrupamento espacial baseado em densidade de aplicações com ruído). Ao contrário do algoritmo k-means o DBSCAN não tenta agrupar todos os pontos de dados no conjunto. O DBSCAN procura zonas com grande densidade de pontos de dados enquanto classificando os pontos que não têm nenhum vizinho direto como pontos atípicos (‘outliers’) ou com ruído. DBSCAN é uma excelente escolha quando lidamos com conjuntos de dados que não estão agrupados linearmente, incluem antes regiões densas com pontos de dados.
O Algoritmo DBSCAN
O algoritmo básico do DBSCAN está muito bem explicado no seu artigo da wikipedia.
- O primeiro passo consiste em definir uma distância ε que define a região de vizinhança (raio) em torno do ponto de dados. Tal como no algoritmo k-means a implementação por definição do scikit-learn do DBSCAN usa como métrica de distância a distância euclidiana, utilizada para calcular a distância entre os pontos de dados. O segundo valor que necessita de ser definido é o número de mínimos de pontos dados que precisam de estar localizados na vizinhança de um ponto de dados para definir essa região como sendo densa (incluindo o ponto de dados em si).
- O algoritmo começa por escolher um ponto de dados aleatoriamente no conjunto de dados para ser o ponto inicial. O DBSCAN procura, então, por outros pontos de dados na região ε em torno do ponto inicial. Supondo que existem, pelo menos, n pontos de dados (com n igual ao número mínimo de pontos de dados mencionados anteriormente) na vizinhança (incluindo o ponto inicial). Neste caso, o ponto inicial e todos outros pontos na região do ponto inicial são definidos como pontos pertencentes ao agrupamento principal. Se existem menos de n pontos de dados na vizinhança do ponto inicial, este é classificado como ponto com ruído ou atípico (no entanto, este ponto pode ser membro de outro agrupamento posteriormente). Neste caso, o algoritmo continua selecionando outro ponto de dados do conjunto de ainda não classificados (i.e. não pertencentes a um agrupamento ou classificados como pontos com ruído) recomeçando o passo 2 do algoritmo.
- Se o agrupamento inicial foi encontrado, então o algoritmo DBSCAN analisa a região ε em torno de cada ponto deste agrupamento. Se a região incluir pelo menos n pontos de dados, então esses pontos são também incluídos no agrupamento, e assim sucessivamente. Se um dos pontos do agrupamento inicial não tiver n pontos na sua vizinhança, destes alguns ainda não foram incluídos em nenhum agrupamento, também serão incluídos no agrupamento (como pontos de fronteira). Nos casos em que os pontos de fronteira pertencem a outros agrupamentos, vão ser associados ao agrupamento do qual menos distam.
- Assim que todos os pontos de dados tiverem sido visitados e classificados como sendo ou parte de um agrupamento, ou ponto com ruído, o algoritmo para.
Ao contrário do algoritmo k-means a dificuldade não se prende com encontrar o número de agrupamentos a encontrar, mas qual é a região mais apropriada para o conjunto de dados. Um método útil para encontrar o valor próprio para o eps é explicado neste artigo de towardsdatascience.com. Em suma, o DBSCAN permite calcular a distância entre cada ponto de dados num conjunto e identificar o seu vizinho mais próximo. É possível depois ordenar pela distância por uma ordem ascendente. Finalmente, podemos olhar para o ponto no gráfico que inicia o segmento de maior declive e realizar uma inspeção visual da evolução do valor do eps, similarmente ao método do ‘cotovelo’ descrito para o caso do k-means. Utilizaremos este método no tutorial.
Agora que sabemos como os nossos algoritmos de agrupamento funcionam e os métodos que podemos aplicar para determinar o número de agrupamentos, aplicaremos estes conceitos ao contexto dos nos conjuntos de dados do Brill’s New Pauly e do jornal Religion. Comecemos por analisar o conjunto de dados DNP_ancient_authors.csv.
Primeiro caso de estudo: Aplicar k-means ao conjunto de dados de autores da antiguidade do Brill’s New Pauly
1. Explorando o conjunto de dados
Antes de começar com o agrupamento, exploremos os dados carregando DNP_ancient_authors.csv para o Python utilizando pandas. Comecemos por imprimir as primeiras cinco linhas e vendo alguma informação e estatísticas sobre o conjunto de dados utilizando os métodos info() e describe().
import pandas as pd
# Carregar o conjunto de dados dos autores que foi armazenado como um ficheiro .csv numa pasta chamada "data" no mesmo diretório que o Jupyter Notebook
df_authors = pd.read_csv("data/DNP_ancient_authors.csv", index_col="authors").drop(columns=["Unnamed: 0"])
# Mostrar a estrutura do conjunto de dados com o método .info() do pandas
print(df_authors.info())
# Mostrar as primeiras cinco filas
print(df_authors.head(5))
# Mostrar algumas estatísticas
print(df_authors.describe())
A saída do método info() deve ter o seguinte aspeto:
<class 'pandas.core.frame.DataFrame'>
Index: 238 entries, Achilles Tatius of Alexandria to Zosimus
Data columns (total 8 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 word_count 238 non-null int64
1 modern_translations 238 non-null int64
2 known_works 238 non-null int64
3 manuscripts 238 non-null int64
4 early_editions 238 non-null int64
5 early_translations 238 non-null int64
6 modern_editions 238 non-null int64
7 commentaries 238 non-null int64
dtypes: int64(8)
memory usage: 16.7+ KB
Como podemos ver os nossos dados consistem em 238 entradas do tipo inteiro. Em seguida, vamos examinar os nossos dados utilizando a saída do método pandas describe().
A saída do df_authors.describe deve ter o seguinte aspeto:
word_count modern_translations known_works manuscripts early_editions early_translations modern_editions commentaries
count 238.000000 238.000000 238.000000 238.000000 238.000000 238.000000 238.000000 238.000000
mean 904.441176 12.970588 4.735294 4.512605 5.823529 4.794118 10.399160 3.815126
std 804.388666 16.553047 6.784297 4.637702 4.250881 6.681706 11.652326 7.013509
min 99.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
25% 448.750000 4.250000 1.000000 1.000000 3.000000 0.000000 4.000000 0.000000
50% 704.000000 9.000000 2.000000 3.000000 5.000000 2.500000 7.000000 1.000000
75% 1151.500000 15.750000 6.000000 6.000000 8.000000 8.000000 14.000000 4.000000
max 9406.000000 178.000000 65.000000 34.000000 28.000000 39.000000 115.000000 43.000000
Podemos verificar que os valores do desvio padrão e da média variam de forma quando comparando a coluna word_count e as outras colunas. Ao trabalhar com métricas como a distância euclideana no algoritmo k-means, as diferentes escalas em cada coluna podem ser problemáticas. Por isso, devemos normalizar os dados antes de aplicar os algoritmos de agrupamento.
Para mais, temos um significativo desvio padrão em cada coluna e uma diferença grande entre o valor do percentil 75 e o valor máximo, particularmente na coluna word_count. Isto indica que é possível existir algum ruído no nosso conjunto de dados, e pode ser necessário eliminar os dados com ruído antes de prosseguirmos com a análise. Para esse efeito, decidimos manter apenas os pontos de dados do conjunto que estão contidos dentro do percentil 90’’.
ninety_quantile = df_authors["word_count"].quantile(0.9)
df_authors = df_authors[df_authors["word_count"] <= ninety_quantile]
2. Inclusão de bibliotecas e funções adicionais
Antes de começarmos com o processo de agrupamento necessitamos de importar todas as bibliotecas necessárias e escrever um conjunto de funções que nos vão auxiliar a produzir os gráficos com os resultados durante a análise. Também vamos utilizar estas funções e bibliotecas no segundo caso de estudo neste tutorial (analisar os dados dos abstracts da publicação Religion). Por isso, mesmo que decida saltar a análise aos dados dos autores da antiguidade, ainda necessita de importar esta funções e bibliotecas para executar o código da segunda parte deste tutorial.
from sklearn.preprocessing import StandardScaler as SS # z-score standardization
from sklearn.cluster import KMeans, DBSCAN # clustering algorithms
from sklearn.decomposition import PCA # dimensionality reduction
from sklearn.metrics import silhouette_score # used as a metric to evaluate the cohesion in a cluster
from sklearn.neighbors import NearestNeighbors # for selecting the optimal eps value when using DBSCAN
import numpy as np
# plotting libraries
import matplotlib.pyplot as plt
import seaborn as sns
from yellowbrick.cluster import SilhouetteVisualizer
A seguinte função vai ajudar-nos a mostrar (e guardar) os gráficos do coeficiente de silhueta.
def silhouettePlot(range_, data):
'''
vamos utilizar esta função para mostrar os gráficos do coeficiente de silhueta e ajudar-nos a avaliar a coesão intra-agrupamento (apenas para o *k*-means)
'''
half_length = int(len(range_)/2)
range_list = list(range_)
fig, ax = plt.subplots(half_length, 2, figsize=(15,8))
for _ in range_:
kmeans = KMeans(n_clusters=_, random_state=42)
q, mod = divmod(_ - range_list[0], 2)
sv = SilhouetteVisualizer(kmeans, colors="yellowbrick", ax=ax[q][mod])
ax[q][mod].set_title("Silhouette Plot with n={} Cluster".format(_))
sv.fit(data)
fig.tight_layout()
fig.show()
fig.savefig("silhouette_plot.png")
A função seguinte vai ajudar-nos a mostrar (e guardar) os gráficos do método do cotovelo.
def elbowPlot(range_, data, figsize=(10,10)):
'''
a função para produzir o gráfico do método do cotovelo vai ajudar-nos a determinar o número adequado de agrupamentos para o nosso conjunto de dados
'''
inertia_list = []
for n in range_:
kmeans = KMeans(n_clusters=n, random_state=42)
kmeans.fit(data)
inertia_list.append(kmeans.inertia_)
# plotting
fig = plt.figure(figsize=figsize)
ax = fig.add_subplot(111)
sns.lineplot(y=inertia_list, x=range_, ax=ax)
ax.set_xlabel("Cluster")
ax.set_ylabel("Inertia")
ax.set_xticks(list(range_))
fig.show()
fig.savefig("elbow_plot.png")
A próxima função vai ajudar a encontrar o valor correto para o eps necessário para o DBSCAN.
def findOptimalEps(n_neighbors, data):
'''
função para encontrar o valor ótimo da distância eps para o DBSCAN: baseada neste artigo: https://towardsdatascience.com/machine-learning-clustering-dbscan-determine-the-optimal-value-for-epsilon-eps-python-example-3100091cfbc
'''
neigh = NearestNeighbors(n_neighbors=n_neighbors)
nbrs = neigh.fit(data)
distances, indices = nbrs.kneighbors(data)
distances = np.sort(distances, axis=0)
distances = distances[:,1]
plt.plot(distances)
A última função progressiveFeatureSelection() implementa um algoritmo básico para selecionar variáveis do nosso conjunto de dados basead no coeficiente de silhueta e agrupamento k-means. Primeiro, o algoritmo identifica a variável com melhor coeficiente de silhueta quando utilizando agrupamento k-means. Depois, treina um novo modelo k-means para cada combinação da variável escolhida inicialmente e cada uma das restantes. Em seguida, escolhe a combinação de variáveis com melhor valor no coeficiente de silhueta. O algoritmo utiliza este par de variáveis para encontrar a combinação ótima destas duas com uma das restantes e assim sucessivamente. O algoritmo continua até descobrir a combinação ótima de n variáveis (onde n é o valor do parâmetro max_features).
Este algoritmo é inspirado por esta discussão no stackexchange.com. No entanto, não será necessário demasiada preocupação em relação a esta implementação; Existem melhores soluções para realizar seleção de variáveis, como demonstrado no paper de Manjoranjan Dash e Huan Liu ‘Feature Selection for Clustering’. Como a maioria dos potenciais algoritmos para seleção de variáveis num contexo não supervisionado não estão implementados no scikit-learn, decidi implementar um, apesar de básico.
def progressiveFeatureSelection(df, n_clusters=3, max_features=4,):
'''
Implementação básica de um algoritmo para seleção de variáveis (agrupamento não supervisionado); inspirada por esta discussão: https://datascience.stackexchange.com/questions/67040/how-to-do-feature-selection-for-clustering-and-implement-it-in-python
'''
feature_list = list(df.columns)
selected_features = list()
# select starting feature
initial_feature = ""
high_score = 0
for feature in feature_list:
kmeans = KMeans(n_clusters=n_clusters, random_state=42)
data_ = df[feature]
labels = kmeans.fit_predict(data_.to_frame())
score_ = silhouette_score(data_.to_frame(), labels)
print("Proposed new feature {} with score {}". format(feature, score_))
if score_ >= high_score:
initial_feature = feature
high_score = score_
print("The initial feature is {} with a silhouette score of {}.".format(initial_feature, high_score))
feature_list.remove(initial_feature)
selected_features.append(initial_feature)
for _ in range(max_features-1):
high_score = 0
selected_feature = ""
print("Starting selection {}...".format(_))
for feature in feature_list:
selection_ = selected_features.copy()
selection_.append(feature)
kmeans = KMeans(n_clusters=n_clusters, random_state=42)
data_ = df[selection_]
labels = kmeans.fit_predict(data_)
score_ = silhouette_score(data_, labels)
print("Proposed new feature {} with score {}". format(feature, score_))
if score_ > high_score:
selected_feature = feature
high_score = score_
selected_features.append(selected_feature)
feature_list.remove(selected_feature)
print("Selected new feature {} with score {}". format(selected_feature, high_score))
return selected_features
De notar que selecionámos n=3 agrupamentos como o padrão para a produção de um modelo de agrupamento k-means na função progressiveFeatureSelection(). No contexto de ajuste de hiperparâmetros avançado (que não faz parte do âmbito deste tutorial) faria sentido treinar a função progressiveFeatureSelection com diferentes valores para o n utilizado para a produção do modelo k-means. Por questões de simplicidade, vamos manter n=3 agrupamentos neste tutorial.
3. Normalizar o conjunto de dados DNP Ancient Authors
Em seguida, inicializamos a função do scikit-learn StandardScaler() para normalizar os nossos dados. Aplicamos a função do scikit-learn StandardScaler(z-score) para projetar a média das colunas para aproximadamente zero e o desvio padrão para um, de modo a ter em conta a diferenças gigantescas entre a coluna word_count e as outras colunas em df_ancient_authors.csv.
scaler = SS()
DNP_authors_standardized = scaler.fit_transform(df_authors)
df_authors_standardized = pd.DataFrame(DNP_authors_standardized, columns=["word_count_standardized", "modern_translations_standardized", "known_works_standardized", "manuscripts_standardized", "early_editions_standardized", "early_translations_standardized", "modern_editions_standardized", "commentaries_standardized"])
df_authors_standardized = df_authors_standardized.set_index(df_authors.index)
4. Seleção de variáveis
Se a tarefa de agrupamento fosse realizada para a totalidade do DNP_ancient_authors.csv com o k-means seria impossível encontrar algum valor razoável para o número de agrupamentos no conjunto de dados. Isto ocorre frequentemente quando trabalhamos com dados reais. No entanto, nestes casos, pode ser pertinente procurar por um sub conjunto de variáveis para nos ajudar a estruturar os dados. Teoricamente, como estamos a lidar com apenas 10 variáveis, poderíamos fazer isto manualmente. Mas como já implementamos um algoritmo básico que nos ajuda a encontrar combinações potencialmente interessantes de variáveis, vamos utilizar a nossa função progressiveFeatureSelection(). Neste tutorial vamos procurar três variáveis que nos parecem interessantes. No entanto, sinta-se à vontade para experimentar valores diferentes de max_features na função progressiveFeatureSelection(), (assim como de números de agrupamentos, n_clusters). A seleção de apenas três variáveis, (assim como n=3 para o número de agrupamentos em cada modelo k-means) foi uma decisão aleatória que levou a resultados promissores inesperados. Isto não significa que não existam outras combinações promissoras que possam ser de valor examinar.
selected_features = progressiveFeatureSelection(df_authors_standardized, max_features=3, n_clusters=3)
Ao correr esta função, determina-se que existem três variáveis known_works_standardized, commentaries_standardized e modern_editions_standardized que podem ter valor para realizar o agrupamento dos nossos dados. Por isso, criamos um novo ‘data frame’ com apenas estas três variáveis.
df_standardized_sliced = df_authors_standardized[selected_features]
5. Escolher o número correto de agrupamentos
Vamos agora aplicar o método do cotovelo e os gráficos do coeficiente de silhuera para obter uma estimativa de quantos agrupamentos devamos utilizar para analisar o nosso conjunto de dados. Vamos limitar-nos a analisar para valores entre dois e dez agrupamentos. É de notar, no entando, que a seleção de variáveis foi realizada para um algoritmo k-means pré-definido para usar n=3 agrupamentos. Por isso, as nossas três variáveis selecionadas já tendem naturalmente para este número de agrupamentos.
elbowPlot(range(1,11), df_standardized_sliced)
O gráfico do método do cotovelo tem este aspeto:
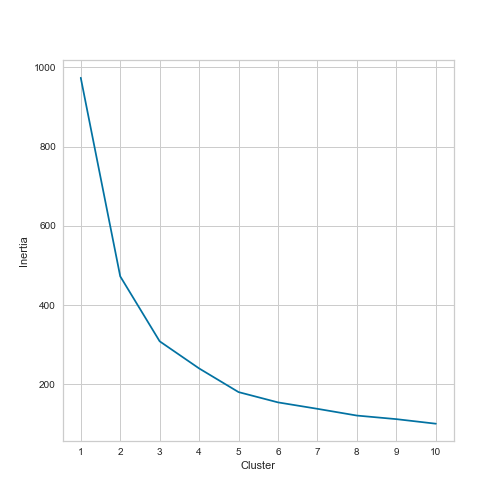
Figura 7: Gráfico do método do cotovelo para o conjunto de dados df_standardized_sliced.
Olhando para o gráfico do método do cotovelo conseguimos encontrar um ‘cotovelo’ em n=3 e n=5 agrupamentos. No entanto, continua a existir o desafio de decidir utilizar três, quatro, cinco ou mesmo seis agrupamentos. Por isso, devemos também olhar para os gráficos do coeficiente de silhueta.
silhouettePlot(range(3,9), df_standardized_sliced)
Os gráficos do coeficiente de silhueta têm o seguinte aspeto:
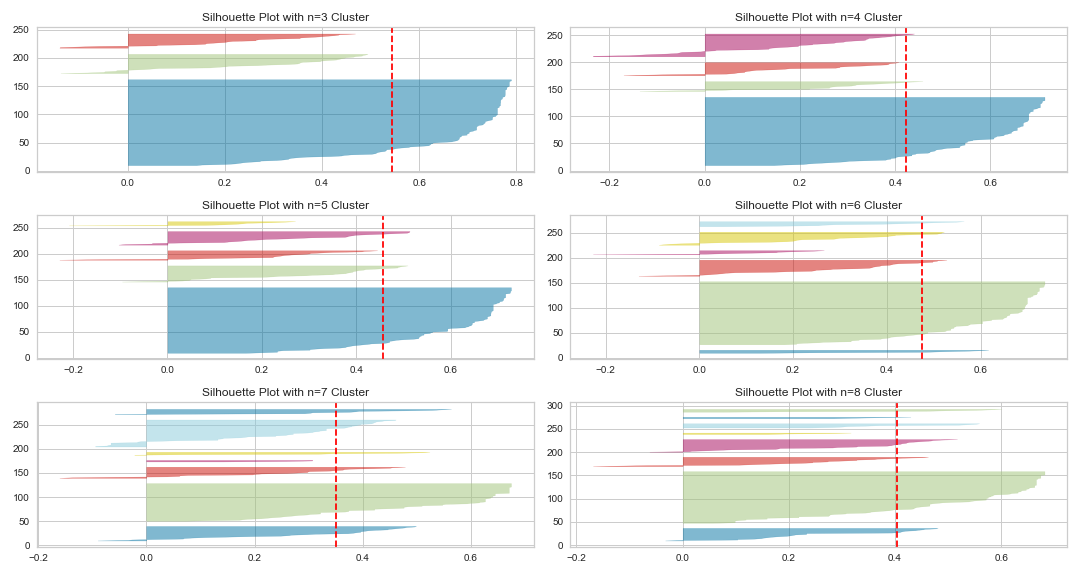
Figura 8: Gráficos do coeficiente de silhueta para o conjunto de dados df_standardized_sliced.
Ao olhar para os valores do coeficiente de silhueta temos uma confirmação da nossa intuição que a escolha de n=3 ou n=5 aparenta ser a escolha correta para o número de agrupamentos. Em particular, o gráfico do coeficiente de silhueta para n=3 agrupamentos tem um valor médio relativamente elevado para o coeficiente de silhueta. No entanto, os outros dois agrupamentos tem um valor bastante inferior à média do valor de silhueta para n=3 agrupamentos. Decidimos então analisar o conjunto de dados com o k-means utilizando n=5 agrupamentos. No entanto, os diferentes tamanhos das ‘facas’ e a sua forma afiada para quer n=3 ou n=5 agrupamentos indicam a existência de um único agrupamento dominante e um conjunto de pequenos e menos coesos agrupamentos.
6. n=5 k-means análise do conjunto de dados DNP Ancient Authors
Podemos agora treinar um modelo k-means para n=5 agrupamentos e representar graficamente os dados utilizando a biblioteca seaborn. Prefiro representar graficamente o resultado do agrupamento em apenas duas dimensões em Python. Para isso, vamos utilizar PCA() (Principal Component Analysis, em português análise de componentes principais) para reduzir a dimensionalidade do nosso conjunto de dados para apenas duas dimensões. PCA é uma ótima maneira de reduzir a dimensionalidade de um conjunto de dados enquanto se preserva a variância das dimensões superiores.
PCA permite-nos reduzir a dimensionalidade original dos dados substancialmente, enquanto retemos a informação de maior importância. No conjunto de variáveis resultantes da aplicação do PCA, os algoritmos de aprendizagem automática — a ser aplicados posteriormente no processo de aprendizagem automática — irão ter maior facilidade em separar os pontos de dados no espaço (necessário para realizar tarefas como deteção de anomalias e agrupamento), enquanto requerem menos recursos computacionais (traduzido da versão disponível do livro Unsupervised Learning Using Python de Arthur A. Patel, O’Reilly Media 2020).
PCA pode ser utilizado para reduzir conjuntos de dados de elevada dimensionalidade por razões computacionais. No entanto, neste contexto apenas queremos utilizar o PCA para representar graficamente o nosso conjunto de dados num espaço bidimensional. Vamos também aplicar o PCA na tarefa de agrupamento textual. Uma grande desvantagem do PCA é que perdemos as nossas variáveis iniciais e criamos outras que são nos um pouco opacas, não nos permitindo olhar para aspetos específicos dos nossos dados (tais como o número de palavras e obras conhecidas).
Antes de utilizar o PCA para representar graficamente os resultados, temos que treinar um modelo k-means para n=5 agrupamentos e um random_state de 42. O último parâmetro permite que os resultados sejam reproduzíveis. 42 é um número arbitrário, sendo que a escolha aqui refere-se ao The Hitchhiker’s Guide to the Galaxy (na versão portuguesa À Boleia Pela Galáxia. Neste livro o número 42 é tido como a resposta para a pergunta definitiva sobre a vida, o universo e tudo mais, o problema é que ninguém sabe qual é a pergunta.). Outro valor para este parâmetro poderia ter sido escolhido.
kmeans = KMeans(n_clusters=5, random_state=42)
cluster_labels = kmeans.fit_predict(df_standardized_sliced)
df_standardized_sliced["clusters"] = cluster_labels
# Utilizar o PCA para reduzir a dimensionalidade
pca = PCA(n_components=2, whiten=False, random_state=42)
authors_standardized_pca = pca.fit_transform(df_standardized_sliced)
df_authors_standardized_pca = pd.DataFrame(data=authors_standardized_pca, columns=["pc_1", "pc_2"])
df_authors_standardized_pca["clusters"] = cluster_labels
# Representar graficamente os agrupamentos
sns.scatterplot(x="pc_1", y="pc_2", hue="clusters", data=df_authors_standardized_pca)
No gráfico correspondente (ver figura 9) podemos claramente distinguir vários agrupamentos nos nossos dados. No entanto, podemos também visualizar aquilo que foi descrito pelos gráficos de silhueta, nomeadamente a existência de um agrupamento denso e dois ou três outros menos coesos com vários pontos de dados que são ruído.
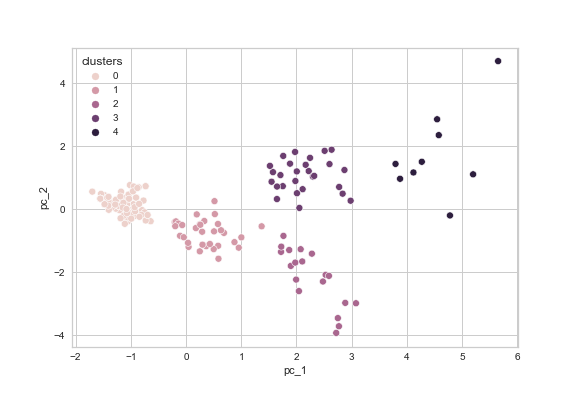
Figura 9: Gráfico final do agrupamento do conjunto de dados df_standardized_sliced produzido com o seaborn.
7. Conclusão
Foi possível observar alguns agrupamentos claros nos nossos dados utilizando o subconjunto de variáveis known_works_standardized, commentaries_standardized, e modern_editions_standardized. Mas o que isto significa? Isto é uma questão que o algoritmo não pode responder. Os algoritmos de agrupamento apenas demonstram que existem agrupamentos específicos sob determinadas condições, neste caso, quando procurando para n=5 agrupamentos com o k-means para o subconjunto de variáveis mencionadas anteriormente. Mas que informação está a ser capturada por estes agrupamentos? Estes permitem-nos conhecer algo sobre os nossos dados? Para responder a esta questão temos que olhar para os membros de cada agrupamento e analisar se o facto de eles estarem agrupados nos dá uma pista sobre aspetos do conjunto de dados que merecem ser mais explorados.
No nosso exemplo, ao olhar para o agrupamento 0 (o mais denso na parte esquerda do nosso gráfico) revela que este agrupamento inclui autores com muito poucas obras conhecidas, poucos comentários, poucas edições modernas, e entradas curtas no DNP (a média do número de palavras é de 513). Isto significa que estão incluídos no agrupamento de autores da antiguidade que são relativamente desconhecidos.
| authors | word_count | modern_translations | known_works | manuscripts | early_editions | early_translations | modern_editions | commentaries |
|---|---|---|---|---|---|---|---|---|
| Achilles Tatius of Alexandria | 383 | 5 | 1 | 2 | 3 | 9 | 2 | 1 |
| Aelianus Tacticus | 350 | 1 | 1 | 0 | 3 | 6 | 1 | 0 |
| Aelianus, Claudius (Aelian) | 746 | 8 | 3 | 6 | 10 | 8 | 7 | 0 |
| Aeneas Tacticus | 304 | 5 | 1 | 1 | 1 | 2 | 6 | 0 |
| Aesop | 757 | 18 | 1 | 6 | 10 | 2 | 11 | 1 |
| Agatharchides of Cnidus | 330 | 2 | 3 | 0 | 4 | 1 | 1 | 0 |
| Agathias | 427 | 4 | 2 | 1 | 2 | 4 | 6 | 0 |
| Alexander of Tralleis | 871 | 4 | 4 | 7 | 3 | 3 | 4 | 2 |
| Ammianus Marcellinus | 573 | 8 | 1 | 3 | 6 | 4 | 6 | 6 |
| Anacreontea | 544 | 3 | 1 | 0 | 1 | 10 | 5 | 0 |
Como podemos observar pela amostra anterior que mostra as primeiras dez entradas do agrupamento 0, os nomes dos autores (excetuando Aesop) suportam mais ou menos a nossa hipótese inicial que estamos a lidar predominantemente com autores cujo trabalho produziu poucas edições modernas, particularmente quando comparados com os autores incluídos no agrupamento 4.
Os autores do agrupamento 4 (o agrupamento menos coeso no topo direito do nosso gráfico) inclui autores conhecidos e extensivamente discutidos, incluindo Platão e Aristófanes, que escreveram vários trabalhos para os quais são famosos e que se mantiveram relevantes ao longo dos séculos, demonstrado pela existência de um número elevado de edições modernas e comentários.
| authors | word_count | modern_translations | known_works | manuscripts | early_editions | early_translations | modern_editions | commentaries |
|---|---|---|---|---|---|---|---|---|
| Aeschylus of Athens | 1758 | 31 | 7 | 5 | 10 | 14 | 15 | 20 |
| Aristophanes of Athens | 1108 | 18 | 11 | 2 | 6 | 30 | 7 | 18 |
| Lucanus, Marcus Annaeus | 1018 | 17 | 1 | 11 | 8 | 15 | 20 | 25 |
| Plato | 1681 | 31 | 18 | 5 | 5 | 0 | 10 | 20 |
| Plutarchus of Chaeronea (Plutarch) | 1485 | 37 | 2 | 2 | 6 | 0 | 15 | 42 |
| Propertius, Sextus | 1443 | 22 | 1 | 5 | 5 | 5 | 24 | 22 |
| Sallustius Crispus, Gaius (Sallust) | 1292 | 17 | 5 | 12 | 7 | 15 | 15 | 16 |
| Sophocles | 1499 | 67 | 8 | 4 | 5 | 0 | 14 | 18 |
| Tacitus, (Publius?) Cornelius | 1504 | 29 | 5 | 6 | 10 | 14 | 31 | 20 |
Se quiserem olhar com mais detalhe para os outros agrupamentos aconselho a explorar o Jupyter Notebook que está disponível neste repositório do GitHub.
Em suma, o nosso agrupamento do conjunto de dados DNP_ancient_authors.csv resultou em alguns agrupamentos promissores, que podem ajudar-nos a desenvolver novas questões de pesquisa. Por exemplo, podemos agora analisar estes agrupamentos aplicando a nossa hipótese sobre a relevância para explorar mais agrupamentos dos autores, baseados nas suas edições iniciais e modernas. No entanto, isto está para lá do âmbito deste tutorial, que tem como preocupação principal introduzir as ferramentas e os métodos para examinar este tipo de questões de pesquisa.
Segundo caso de estudo: agrupamento de dados textuais
A segunda secção deste tutorial tratará de dados textuais, nomeadamente os abstracts retirados do website da publicação Religion. Vamos tentar agrupar os abstracts através das suas palavras, adotando a representação de um vetor TF-IDF (sendo um acrónimo para Term Frequency - Inverse Document Frequency, em português: frequência do termo - inverso da frequência nos documentos).
1. Carregar o conjunto de dados & análise exploratória dos dados
Utilizando um método similar aquele que usado para analizar o conjunto de dados DNP_ancient_authors.csv, vamos primeiro carregar RELIGION_abstracts.csv para o nosso programa e ver algumas estatísticas sumárias.
df_abstracts = pd.read_csv("data/RELIGION_abstracts.csv").drop(columns="Unnamed: 0")
df_abstracts.info()
df_abstracts.describe()
O resultado do método describe() deve ser algo parecido com isto:
title abstract link volume
count 701 701 701 701
unique 701 701 701 40
top From locality to (...) https://www.tandfonline.com/doi/abs/10.1006/reli.1996.9998 Titel anhand dieser DOI in Citavi-Projekt übernehmen https://www.tandfonline.com/loi/rrel20?treeId=vrrel20-50
freq 1 1 1 41
Ao contrário do conjunto de dados anterior, estamos a lidar agora com variáveis em que cada observação é única.
2. Vetorização TF-IDF
De modo a processar os dados textuais com os nossos algoritmos de agrupamento necessitamos de converter os textos em vetores. Para este propósito utilizamos a implementação do scikit-learn de vetorização TF-IDF. Para uma boa introdução ao funcionamento do TF-IDF ver este excelente tutorial da Melanie Walsh.
Passo opcional: lematização
Como um passo opcional implementei uma função chamada lemmatizeAbstracts() que lematiza os abstracts utilizando spaCy. Considerando que não estamos interessados em similaridades estilísticas entre os abstracts este passo ajuda a reduzir a quantidade de palavras no nosso conjunto de dados. Como parte da função de lematização também limpados o texto de toda pontuação e ruído tal como parênteses. Na análise a realizar em seguida utilizamos a versão lematizada dos abstracts. No entanto, é possível continuar a usar os textos originais e passar o passo da lematização, sendo que isto pode levar a resultados diferentes.
# Lematização (passo opcional)
import spacy
import re
nlp = spacy.load("en_core_web_sm")
def lemmatizeAbstracts(x):
doc = nlp(x)
new_text = []
for token in doc:
new_text.append(token.lemma_)
text_string = " ".join(new_text)
# getting rid of non-word characters
text_string = re.sub(r"[^\w\s]+", "", text_string)
text_string = re.sub(r"\s{2,}", " ", text_string)
return text_string
df_abstracts["abstract_lemma"] = df_abstracts["abstract"].apply(lemmatizeAbstracts)
df_abstracts.to_csv("data/RELIGION_abstracts_lemmatized.csv")
Decidi guardar uma nova versão lematizada dos nossos abstracts chamada RELIGION_abstracts_lemmatized.csv. Isto impede ter que realizar a lematização novamente sempre que o notebook é reiniciado.
Vetorização TF-IDF
O primeiro passo é instanciar o nosso modelo TF-IDF passando-lhe o argument (parâmetro) para ignorar ‘stop words’ (i.e. termos comuns normalmente removidos no processamento de texto. Estes termos são removidos uma vez que não adicionam nenhum significado adicional ao texto. Alguns exemplos de ‘stop words’ portuguesas seriam: com, de.). O segundo passo é bastante similar ao treino do nosso modelo k-means no exemplo anterior. Passamos os abstracts do nosso conjunto de dados ao vetorizador de modo a converter os mesmos ao formato vetorial esperado pela implementação. Por enquanto, não estamos a passar nenhuns argumentos adicionais. Finalmente, criamos um objeto DataFrame do pandas para guardar a referência para matriz TF-IDF dos nossos dados textuais.
from sklearn.feature_extraction.text import TfidfVectorizer
tfidf = TfidfVectorizer(stop_words="english")
df_abstracts_tfidf = tfidf.fit_transform(df_abstracts["abstract_lemma"])
Quando imprimimos o objeto df_abstracts_tfidf, podemos verificar que a nossa matriz inicial é enorme e inclui mais de 8000 mil palavras do nosso vocabulário geral de 701 abstracts. Isto é obviamente demasiado, não apenas de uma perspetiva computacional, mas também porque os algoritmos de agrupamento tal como o k-means tornam-se menos eficientes devido ao chamado ‘curse of dimensionality’ (em português, maldição da dimensionalidade. É um regra empírica que diz que um aumento no número de dimensões dos dados (i.e. o espaço de análise torna-se mais esparso) o número de pontos de dados necessários para produzir um modelo útil aumenta exponencialmente.). Por isso, temos que reduzir o número de variáveis significativamente.
Para o fazer, vamos primeiro criar uma nova versão dos nossos dados vetorizados utilizando o TF-IDF. Desta vez, no entanto, parametrizamos o vetorizador para apenas selecionar um conjunto reduzido de 250 variáveis. Vamos também parametrizar o modelo para apenas considerar palavras do vocabulário que aparecem em pelo menos 5 documentos diferentes, mas não em mais de 200. Adicionamos também a possibilidade de incluir palavras e bigramas (tais como século 19). Finalmente, o modelo deve remover do texto quaisquer acentos.
Na segunda etapa, utilizemos a análise dos componentes principais (PCA), desta vez para reduzir a dimensionalidade do nosso conjunto de dados de 250 para 10 dimensões.
# Criar uma nova matriz TF-IDF
tfidf = TfidfVectorizer(stop_words="english", ngram_range=(1,2), max_features=250, strip_accents="unicode", min_df=10, max_df=200)
tfidf_religion_array = tfidf.fit_transform(df_abstracts["abstract_lemma"])
df_abstracts_tfidf = pd.DataFrame(tfidf_religion_array.toarray(), index=df_abstracts.index, columns=tfidf.get_feature_names())
df_abstracts_tfidf.describe()
3. Redução de dimensionalidade utilizando PCA
Como foi mencionado anteriormente vamos agora aplicar o PCA() para reduzir a dimensão dos dados de d=250 para d=10, de modo a ter em conta a maldição da dimensionalidade no treino do k-means. Tal como a escolha de n=3 max_features durante a análise do nosso conjunto de dados dos autores da antiguidade, também a escolha da dimensionalidade d=10 agora foi uma escolha aleatória que calhou produzir resultados promissores. No entanto, existe liberdade para mudar estes parâmetros, enquanto se conduz uma forma mais elaborada de ajuste de hiperparâmetros. Talvez poderá encontrar valores para estes parâmetros que resultem numa forma mais eficaz de agrupar os dados. Por exemplo, poderá querer usar um ‘scree plot’ para descobrir o número optimal de componentes principais para o PCA, de uma forma que é de todo similar ao método do cotovelo no contexto do k-means.
# Utilizar PCA para reduzir a dimensionalidade
pca = PCA(n_components=10, whiten=False, random_state=42)
abstracts_pca = pca.fit_transform(df_abstracts_tfidf)
df_abstracts_pca = pd.DataFrame(data=abstracts_pca)
4. Aplicar o agrupamento k-means a dados textuais
Em seguida, tentamos encontrar um método razoável para agrupamento dos abstracts utilizando o k-means. Tal como no conjunto de dados DNP_ancient_authors.csv, comecemos por encontrar o número correto de agrupamentos aplicando o método do cotovelo e o coeficiente de silhueta.
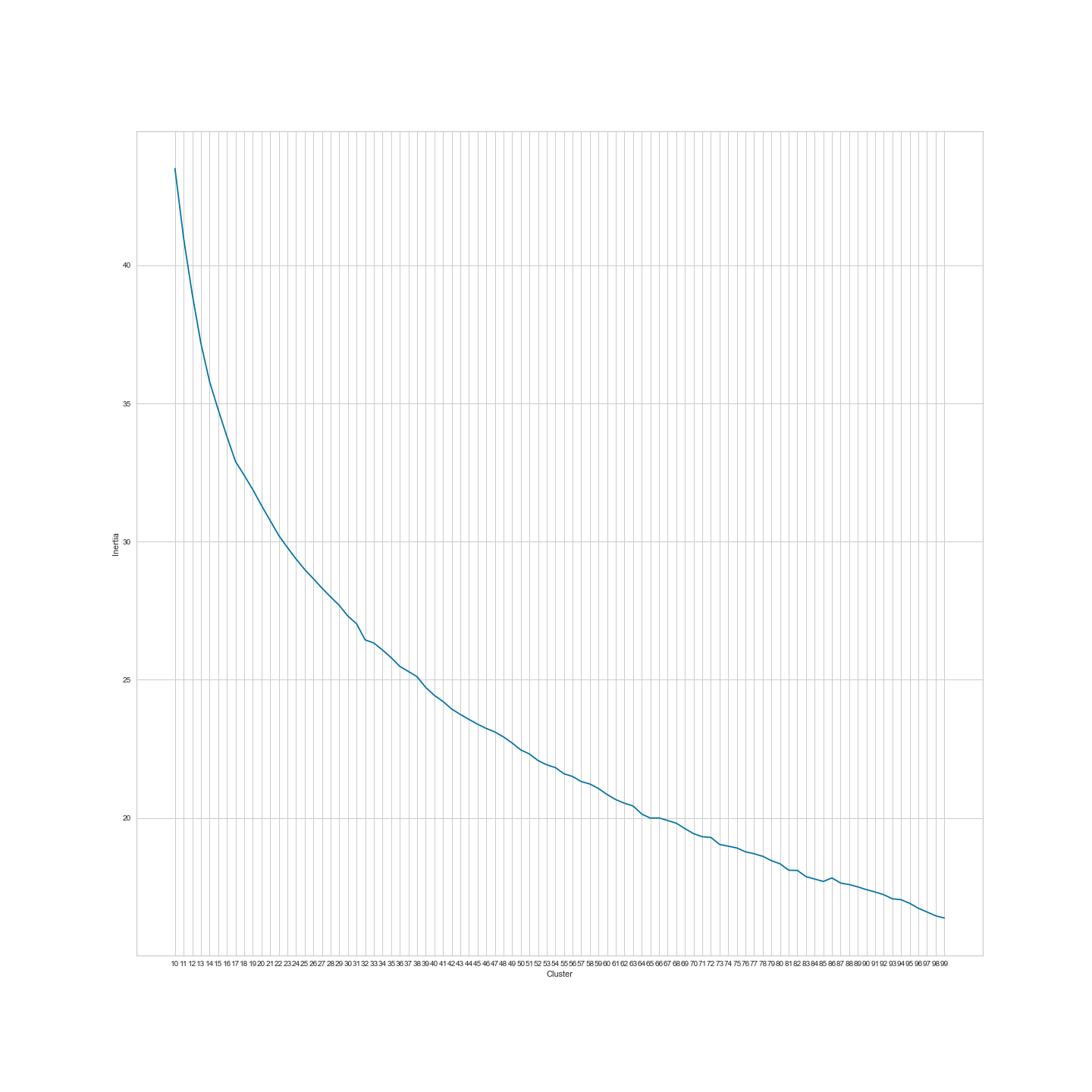
Figura 10: Gráfico do método de cotovelo entre 3 e 99 agrupamentos.
Como podemos ver, não existe nenhum ‘cotovelo’ na nossa representação gráfica. Isto apenas significa que não existem nenhuns agrupamentos grandes no nosso conjunto de dados RELIGION_abstacts.csv. Seria provável que uma publicação tal como a Religion, que cobre um vasto espectro de fenómenos (que estão todos, claro, relacionados com religião) tivesse apenas alguns agrupamentos temáticos? Provavelmente não. Por isso, saltaremos os gráficos do coeficiente de silhueta (uma vez que não existe nenhum valor provável para tão grande número de possíveis agrupamentos) e treinaremos apenas o modelo k-means para n=100 agrupamentos para avaliar os resultados.
kmeans = KMeans(n_clusters=100, random_state=42)
abstracts_labels = kmeans.fit_predict(df_abstracts_pca)
df_abstracts_labeled = df_abstracts.copy()
df_abstracts_labeled["cluster"] = abstracts_labels
Em seguida, avaliamos os resultados imprimindo alguns dos títulos dos artigos de agrupamentos escolhidos de forma aleatória. Por exemplo, quando analisando os títulos do agrupamento 75, podemos verificar que todos os artigos estão relacionados com budismo Teravada, Karma, e a sua perceção no ‘ocidente’.
df_abstracts_labeled[df_abstracts_labeled["cluster"] == 75][["title", "cluster"]]
| title | cluster | |
|---|---|---|
| 210 | Checking the heavenly ‘bank account of karma’: cognitive metaphors for karma in Western perception and early Theravāda Buddhism | 75 |
| 211 | Karma accounts: supplementary thoughts on Theravāda, Madhyamaka, theosophy, and Protestant Buddhism | 75 |
| 258 | Resonant paradigms in the study of religions and the emergence of Theravāda Buddhism | 75 |
O agrupamento 15 inclui artigos relacionados com o corpo e a sua destruição:
df_abstracts_labeled[df_abstracts_labeled["cluster"] == 15][["title", "cluster"]]
| title | cluster | |
|---|---|---|
| 361 | Candanbālā’s hair: Fasting, beauty, and the materialization of Jain wives | 15 |
| 425 | Monkey kings make havoc: Iconoclasm and murder in the Chinese cultural revolution | 15 |
| 623 | Techniques of body and desire in Kashmir Śaivism | 15 |
| 695 | Body-symbols and social reality: Resurrection, incarnation and asceticism in early Christianity | 15 |
Para ser justo, outros agrupamentos são mais difíceis de interpretar. Um bom exemplo disso é o agrupamento 84. No entanto, mesmo no caso do agrupamento 84 aparenta existir um padrão, nomeadamente que todos os artigos são relacionados com pesquisadores famosos ou trabalhos no estudo da religião, tais como Durkheim, Tylor, Otto, Said, etc.
df_abstracts_labeled[df_abstracts_labeled["cluster"] == 84][["title", "cluster"]]
| title | cluster | |
|---|---|---|
| 80 | Latin America 1520–1600: a page in the history of the study of religion | 84 |
| 141 | On elves and freethinkers: criticism of religion and the emergence of the literary fantastic in Nordic literature | 84 |
| 262 | Is Durkheim’s understanding of religion compatible with believing? | 84 |
| 302 | Dreaming and god concepts | 84 |
| 426 | Orientalism, representation and religion: The reality behind the myth | 84 |
| 448 | The Science of Religions in a Fascist State: Rudolf Otto and Jakob Wilhelm Hauer During the Third Reich | 84 |
| 458 | Religion Within the Limits of History: Schleiermacher and Religion—A Reappraisal | 84 |
| 570 | Cognitive and Ideological Aspects of Divine Anthropomorphism | 84 |
| 571 | Tylor’s Anthropomorphic Theory of Religion | 84 |
| 614 | ‘All my relatives’: Persons in Oglala religion | 84 |
| 650 | Colloquium: Does autonomy entail theology? Autonomy, legitimacy, and the study of religion | 84 |
Como podem verificar, mesmo uma implementação simples do k-means para dados textuais sem otimização de variáveis resulta num modelo k-means que apesar das suas limitações, é capaz de nos assistir ao fazer um trabalho de um sistema básico de recomendações. Por exemplo, podemos utilizar o nosso modelo treinado de k-means para sugerir artigos a visitantes do nosso website baseados nas suas leituras anteriores. Claro que também podemos utilizar o nosso modelo durante análise exploratória dos dados para mostrar os agrupamentos temáticos discutidos na Religion.
No entanto, como é possível verificar por este exemplo é bastante difícil realizar o agrupamento e o resultante contém pontos de ruído ou agrupamentos com muito poucos artigos, aparenta fazer mais sentido aplicar um algoritmo de agrupamento diferente e avaliar os seus resultados.
5. Aplicar agrupamento DBSCAN a dados textuais
Apesar do agrupamento k-means já ter resultado em algumas descobertas de valor pode ser ainda interessante aplicar outro algoritmo de agrupamento como o DBSCAN. O DBSCAN exclui ruído e valores atípicos dos nossos dados, o que significa que se foca nas regiões que devem por direito ser chamadas densas.
Utilizaremos a versão reduzida d=10 do conjunto de dados Religion_abstracts.csv, que permite a utilização da distância euclidiana como métrica. Se utilizássemos a matriz TF-IDF inicial com mais de 250 variáveis, teríamos de considerar mudar a métrica para a similaridade do cosseno, sendo melhor a lidar com matrizes esparsas, como são os nossos dados textuais.
O primeiro passo será utilizar a nossa função findOptimalEps() para descobrir qual é o valor de eps mais indicado para os nossos dados.
findOptimalEps(2, df_abstracts_tfidf)
Como podemos notar pela figura 11, o gráfico da variação do eps sugere escolher um valor entre 0.2 e 0.25.
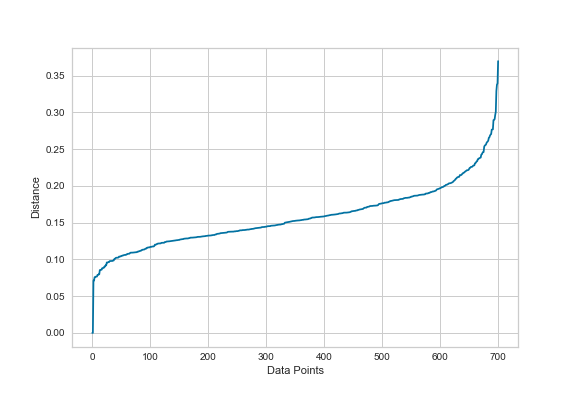
Figura 11: Gráfico de variação do eps para o conjunto de dados dos abstracts.
Selecionaremos para o valor do eps 0.2 e vamos treinar a instância do nosso modelo DBSCAN.
dbscan = DBSCAN(eps=0.2, metric="euclidean")
dbscan_labels = dbscan.fit_predict(df_abstracts_pca)
df_abstracts_dbscan = df_abstracts.copy()
df_abstracts_dbscan["cluster"] = dbscan_labels
df_abstracts_dbscan["cluster"].unique()
Como podemos ver quando olhado para os resultados do DBSCAN no Jupyter Notebook, utilizar o modelo DBSCAN nestas circunstâncias resulta em apenas quatro agrupamentos e uma vasta quantidade de pontos de dados classificados como ruído (-1) com mais de 150 entradas e um grande agrupamento com mais de 500 entradas (agrupamento 0). Estes agrupamentos estão representados graficamente na figura 12 (utilizando um conjunto de dados com a dimensionalidade reduzida utilizando PCA), aqui os nossos resultados não conclusivos são ainda mais visíveis. Neste caso, deveríamos considerar utilizar a matriz TF-IDF inicial com a distância do cosseno.
Mesmo tendo em conta as limitações, a versão atual do modelo DBSCAN aparenta dar-nos algumas descobertas promissoras, como, por exemplo, o agrupamento 3, que inclui artigos relacionados com género e mulheres em diferentes religiões:
df_abstracts_dbscan[df_abstracts_dbscan["cluster"] == 1][["title", "cluster"]]
| title | cluster | |
|---|---|---|
| 154 | Lifelong minority religion: routines and reflexivity: A Bourdieuan perspective on the habitus of elderly Finnish Orthodox Christian women | 1 |
| 161 | Quiet beauty: problems of agency and appearance in evangelical Christianity | 1 |
| 388 | Renunciation feminised? Joint renunciation of female–male pairs in Bengali Vaishnavism | 1 |
| 398 | Conclusion: Construction sites at the juncture of religion and gender | 1 |
| 502 | Gender and the Contest over the Indian Past | 1 |
| 506 | Art as Neglected ‘Text’ for the Study of Gender and Religion in Africa | 1 |
| 507 | A Medieval Feminist Critique of the Chinese World Order: The Case of Wu Zhao (r. 690–705) | 1 |
| 509 | Notions of Destiny in Women’s Self-Construction | 1 |
| 526 | The Fundamental Unity of the Conservative and Revolutionary Tendencies in Venezuelan Evangelicalism: The Case of Conjugal Relations | 1 |
| 551 | Hindu Women, Destiny and Stridharma | 1 |
| 644 | The women around James Nayler, Quaker: A matter of emphasis | 1 |
| 668 | Women as aspects of the mother Goddess in India: A case study of Ramakrishna | 1 |
O agrupamento número 2, por sua vez, está relacionado com crença e ateísmo:
df_abstracts_dbscan[df_abstracts_dbscan["cluster"] == 2][["title", "cluster"]]
| title | cluster | |
|---|---|---|
| 209 | Three cognitive routes to atheism: a dual-process account | 2 |
| 282 | THE CULTURAL TRANSMISSION OF FAITH Why innate intuitions are necessary, but insufficient, to explain religious belief | 2 |
| 321 | Religion is natural, atheism is not: On why everybody is both right and wrong | 2 |
| 322 | Atheism is only skin deep: Geertz and Markusson rely mistakenly on sociodemographic data as meaningful indicators of underlying cognition | 2 |
| 323 | The relative unnaturalness of atheism: On why Geertz and Markússon are both right and wrong | 2 |
| 378 | The science of religious beliefs | 2 |
| 380 | Adaptation, evolution, and religion | 2 |
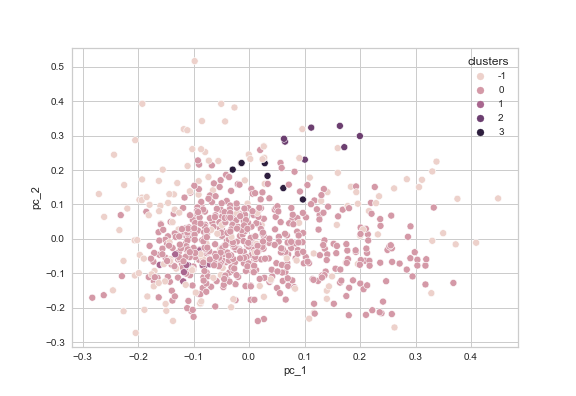
Figura 12: Agrupamentos obtidos pelo DBSCAN para um eps = 0.2 para uma versão reduzida utilizando PCA do conjunto de dados dos abstracts.
Apesar do agrupamento ser longe de perfeito neste caso, produziu alguma informação de valor, que poderia ser utilizada em combinação com os resultados mais promissores do agrupamento k-means. Também poderia ser pertinente continuar a ajustar os parâmetros e a testar diferentes subconjuntos de variáveis (reduzidos, não reduzidos, e talvez adicionar alguma seleção de variáveis adicional para escolher termos promissores, etc.) para atingir melhores resultados com o DBSCAN. Claro que também se poderia aplicar outros algoritmos de agrupamento e depois combinar os resultados.
Como um próximo passo, podíamos desenvolver a ideia de construir um sistema de recomendação básico que sugere um artigo com tópicos similares com base em anteriores leituras. Este sistema de recomendação poderia considerar o agrupamento k-means, mas também incluir sugestões feitas pelo DBSCAN e potencialmente outros algoritmos de agrupamento. Quando aplicados em combinação os resultados bastante insatisfatórios do DBSCAN podem ser menos problemáticos uma vez que são utilizados apenas como informação adicional.
Claro que nós pesquisadores das humanidades provavelmente utilizaremos estas técnicas como parte da nossa pesquisa durante a fase da análise exploratória dos dados. Neste caso, combinar resultados de diferentes algoritmos de agrupamento pode ajudar-nos a descobrir estruturas e agrupamentos temáticos nos nossos dados. Estas descobertas podem levar a novas questões de pesquisa. Por exemplo, pode existir um agrupamento específico nos dados dos abstracts da publicação Religion que inclui mais artigos que outros agrupamentos, indicando um foco temático em particular desta publicação que pode ser de analisar de modo a ter uma visão geral das tendências no estudo da religião nas últimas décadas
Sumário
Espero que tenha mostrado que o agrupamento (clustering) é um passo valioso na análise exploratória dos dados que nos permite ganhar novos pontos de vista sobre os nossos dados.
O agrupamento dos conjuntos de dados DNP_ancient_authors.csv e RELIGION_abstracts.csv fornece resultados decentes e permitiu identificar agrupamentos razoáveis de autores e artigos nos dados. No caso do conjunto de dados dos abstracts construímos mesmo um sistema de recomendações básico para nos assistir na procura de novos artigos em tópicos similares. No entanto, a discussão dos resultados também ilustrou que existe sempre espaço para outras interpretações e que nem todos os agrupamentos têm de fornecer conhecimento novo sobre a perspetiva da investigação (ou humana). Apesar da ambiguidade geral de aplicar algoritmos de aprendizagem automática, as nossas análises demonstraram que o k-means e o DBSCAN são boas ferramentas que ajudam a desenvolver, ou suportar empiricamente, novas questões de pesquisa. Além disso, podem também ser implementados para tarefas mais práticas, como por exemplo, na procura de artigos relacionados com um tópico específico.
Bibliografia
- Géron, Aurélien. Hands-on machine learning with scikit-Learn, Keras, and TensorFlow. Concepts, tools, and techniques to build intelligent systems, 2nd ed. Sebastopol: O’Reilly, 2019.
- Mitchell, Ryan. Web scraping with Python. Collecting more data from the modern web, 1st ed. Sebastopol: O’Reilly, 2018.
- Patel, Ankur A. Hands-on unsupervised learning using Python: How to build applied machine learning solutions from unlabeled data, 1st ed. Sebastopol: O’Reilly, 2019.
Notas de rodapé
-
Para uma boa introdução ao uso de requests e web scraping ver os artigos correspondentes no Programming Historian, como, por exemplo, Introduction to Beautiful Soup ou livros tais como Mitchell (2018). ↩
-
No entanto, existem alguns casos em que o agrupamento k-means pode falhar em identificar agrupamentos nos nossos dados. Por isso, é normalmente recomendado utilizar vários algoritmos de agrupamento. Uma boa ilustração das limitações do agrupamento k-means pode ser visto nos exemplos contidos nesta hiperligação para o website do scikit-learn, particularmente o segundo gráfico na primeira fila. ↩